Having been unable to find an existing solution for my case (3Ds Max + MaxScript) I have “invented” (On the internet everything is already invented if you search enough… I didn’t search enough) an algorithm to fix a 3D mesh issue where some of its vertices went out of symmetry.
The problem
Imagine that we have a 3D mesh that is supposed to be symmetrical: for example, a finished character that needs additional symmetrical adjustments. Or imagine it is time to create morph targets (blend shapes) and having a nice symmetrical head mesh would save you precious time. One condition is that you CAN’T break the mesh’s topology, because UV mapping is already done and/or morph targets depend on the original topology.
Then, for some unfortunate reason, some vertices are out of symmetry.
This could be fixed manually with the tedious process of copying a vertex coordinate, multiplying the X by -1 and pasting it to the other vertex that you identify visually as being the symmetrical pair. But this is very slow, and with more than 10 vertices, it is simply a nightmare. Today, we know how to code!
The starting point

The simplest case to pair vertices is just comparing the coordinates. That’s what the 3Ds Max tool “Symmetry Tools” does. In order to know if two vertices are symmetrical, you need to do this:
//pseudo-code: v is our array of vertices, i and j are indices reflected_Pos = v[i] * vector(-1,1,1) d = distance from reflected_Pos to v[j] if (d < Tolerance) then We Found our Brother!
We are assuming we want symmetry on the X-axis. Multiplying a vertex position by a Vector (-1, 1,1) we get the position mirrored. Then, calculating the distance to the other vertex, we can detect if they are symmetrical pairs if distance = 0 or less than Tolerance. But if Tolerance is too high, this quickly breaks.
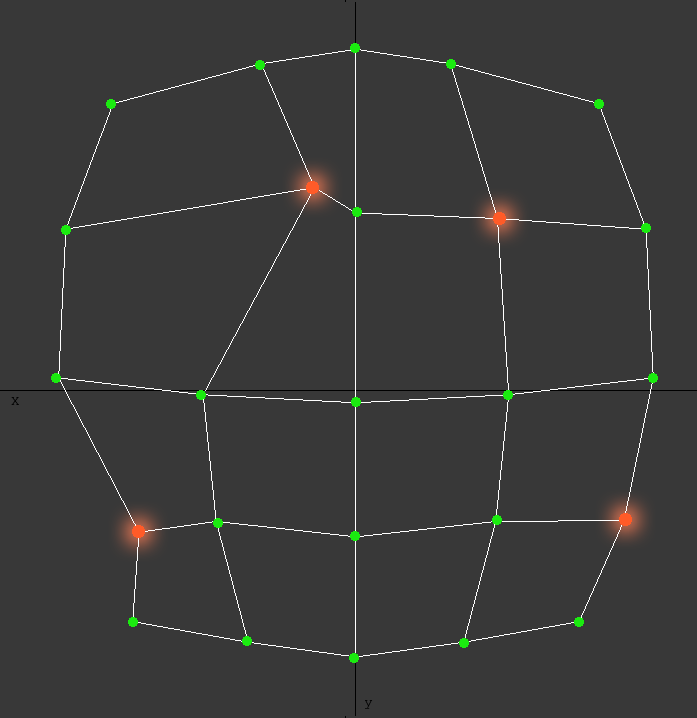
Let’s use our instincts, and take a second look at our first image. How does our brain know which vertices should be paired?
The solution
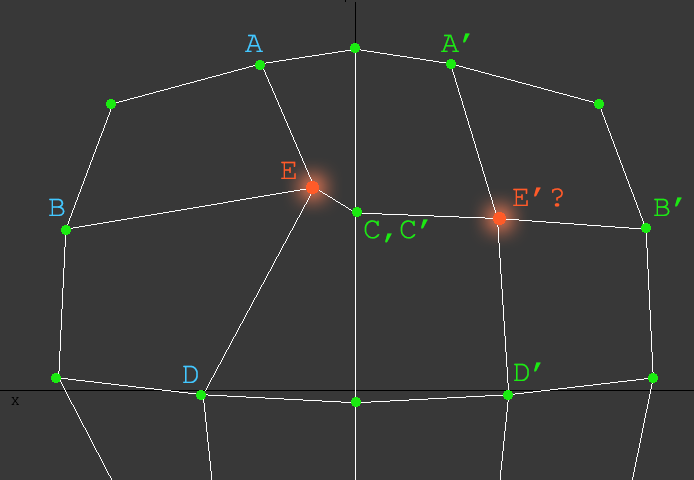
The answer is because we are instinctively comparing their relationship with neighbor vertices. So from the image above we can pair E with E’, since all the connections of E correspond to the same connections of E’ in the mirrored side.
E.connections = A, B, C, D E'.connections = A', B', C', D'
Note that C and C’ are special cases, since the X is zero we can (and should) say that the vertex C is paired to itself.
Now your mind will start finding many cases where this will not work! And that’s true. This method is to find the best solution, not the perfect one. Sometimes the solution simply doesn’t exist.
The next most immediate issue will come when some of the neighbor vertices are also unpaired.
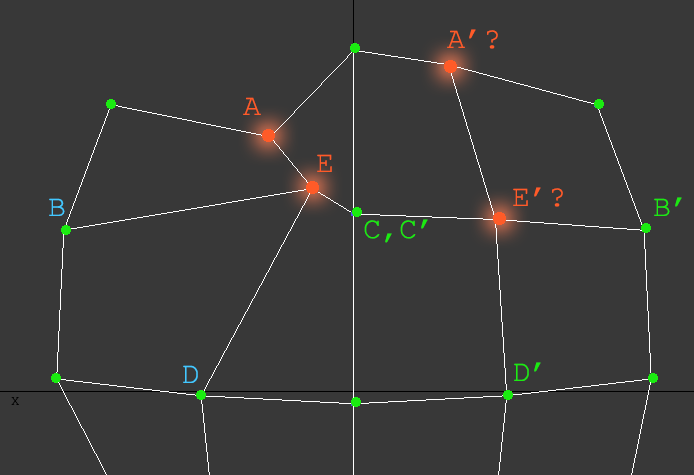
When we are testing for E and E’ it may happen that we don’t know if A and A’ are pairs or not. What to do? Just don’t care… or wait, that’s useful info too.
E.connections = B, C, D, (1 unpaired) E'.connections = B', C', D', (1 unpaired)
Don’t try to find E‘s mirrored brother (E’), just find the best candidate to be E‘s mirrored brother. Then if we have two potential candidates to be E’, with the same set of connections (but the first one has 2 unpaired connections and the second one has 1 unpaired connection), the second one wins the contest because it best matches the characteristics of E.
Letting our thoughts fly, this can lead us to generalize and look for other characteristics of the vertices that could be mirrored and added to this “description” such as normals, skin weights… but let’s keep it simpler for now and for good.
The code
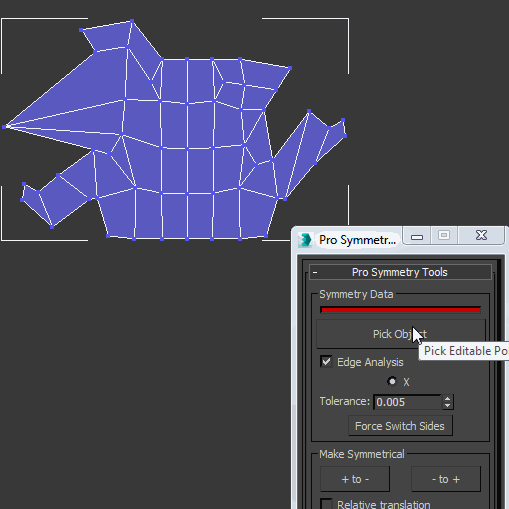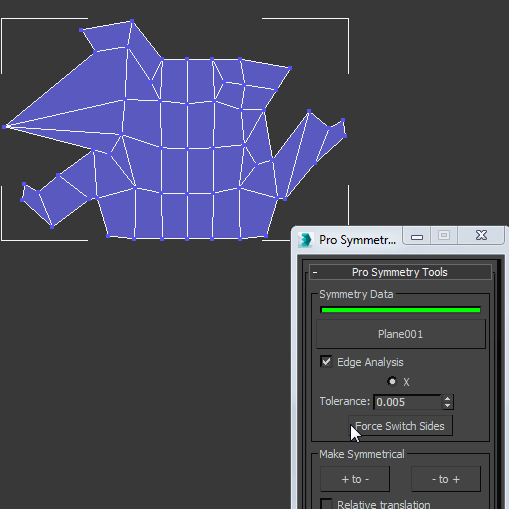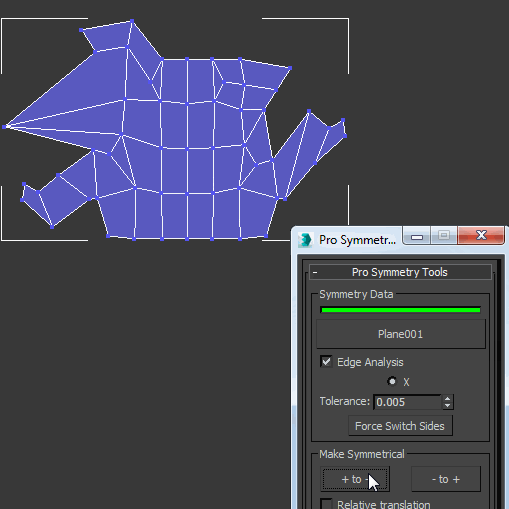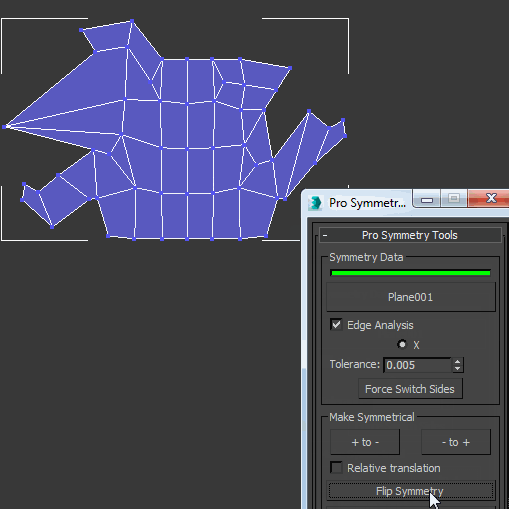
Let’s see our symmetry fixer working now. It does it with passes, and for every pass that pairs are found more useful connections will be used on the next pass until it runs out of good findings.
NOTE: I have to admit I have failed writing a pseudo code before linking it to the source, but after rewriting it 2 times I never was satisfied with the complexity of the text. So, I’ll invite you to take a better look at the working source.
The implementation I did was for 3Ds Max using MaxScript, a tool that I call proSymmetryTool that also adds more functionality for 3Ds Max users that I plan to talk more about later in this blog. Now anyone can see or download it for free here on Github. Our function of interest is “function FindPairs EPolyObj” and for convenience, I have extracted it here as a gist. But I hope with the explanation above in this article you can have fun implementing this algorithm yourself in any other language. Ask me anything in the comments section.